L’investitore in certificati sente spesso parlare di correlazione e in questo articolo voglio chiarire alcuni concetti riguardo al termine statistico (e non al generico termine correlazione, sinonimo di corrispondenza, legame) e spiegare alcuni grafici che a volte accompagnano gli articoli.

Come abbiamo visto anche in un recente Webinar, ad un investitore in certificati interessa la correlazione:

• tra i sottostanti di uno stesso prodotto, poiché la presenza di sottostanti debolmente correlati (o addirittura negativamente correlati) permette la costruzione di prodotti che offrono maggior rendimento;

• tra i sottostanti dei diversi certificati in portafoglio, poiché lo scopo di un portafoglio è proprio quello di diversificare il rischio. L’andamento dei prezzi è uno dei rischi, un altro è quello di credito che può essere ridotto diversificando per emittente.

I dati a nostra disposizione sono i prezzi, ma certe relazioni tra variabili (azioni, indici, ETF) vengono meglio comprese passando ai rendimenti. Vediamo per esempio il primo grafico, con 2 asset che si muovono in maniera estremamente simile, ma la cui correlazione lineare è pari a 0.12. Come qualcuno ha individuato, la seconda serie non è altro che la prima serie spostata di t periodi. Il fatto che le due serie abbiano un trend comune le fa vedere come correlate e solo se passiamo ai rendimenti, ovvero togliamo il trend dalle due serie, possiamo fare un’analisi della loro correlazione.

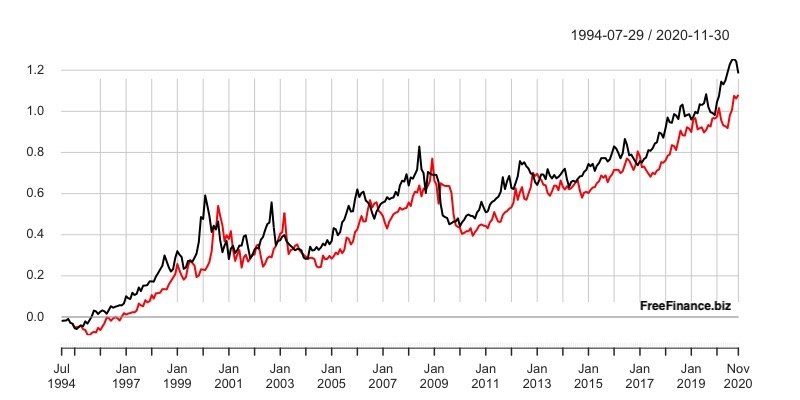
Il coefficiente di correlazione lineare indica la tendenza che hanno due variabili (X e Y) a variare insieme, ovvero, a covariare. Per quanto riguarda il tipo di relazione tra il movimento delle due variabili essa può essere lineare o non lineare.

La relazione è di tipo lineare se quando è rappresentata su assi cartesiani, si avvicina alla forma di una retta. Dai valori della varianza e della covarianza delle variabili si ottiene il coefficiente di correlazione lineare che è standardizzato e può assumere valori che vanno da –1.00 (correlazione perfetta negativa) e +1.00 (correlazione perfetta positiva). Una correlazione uguale a 0 indica che tra le due variabili non vi è alcuna relazione lineare… ma può essere di tipo diverso.

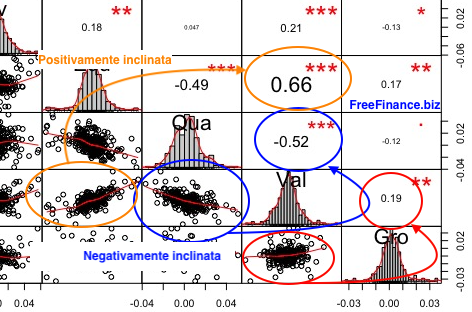
Vediamo un esempio tratto da una matrice di correlazione in cui abbiamo valori positivi o negativi riscontrabili visivamente da una inclinazione positiva o negativa della nuvola di punti. Più questa nuvola di punti ha una forma allungata e sottile maggiore sarà il valore in termini assoluti della correlazione.

Il valore della correlazione è costante? Se analizziamo un sottogruppo di dati (una finestra) e poi muoviamo la finestra nel tempo possiamo vedere come cambi il coefficiente di correlazione, si parla in questo caso di rolling correlation (a finestra mobile). Generalmente si utilizzano dati mensili, ma a volte non si hanno a disposizione serie storiche lunghe o si vuole un grafico maggiormente reattivo. La scelta di rendimenti giornalieri rende il grafico molto reattivo, ma i rendimenti giornalieri potrebbero non essere molto significativi, soprattutto se si confrontano asset quotati su mercati con orari diversi. La scelta della lunghezza della finestra mobile incide sui risultati, con poche osservazioni abbiamo un grafico molto erratico mentre con periodi più lunghi un grafico meno sensibile ai cambiamenti recenti. Nell’ultima immagine vediamo la differenza tra la correlazione (dati mensili) a 12 e 48 mesi di due indici con correlazione media di 0.88.

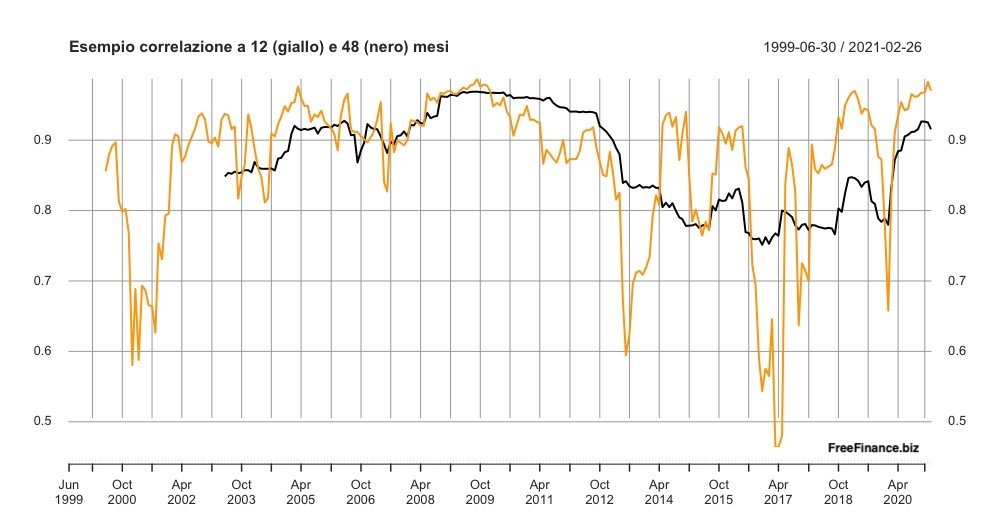
Per formule e rapporti tra covarianza, correlazione e beta rimando agli articoli sulla correlazione e il beta sul mio blog.